UNIDAD 5. ONDAS MECÁNICAS
5.1 Tipos de ondas mecánicas
Una Onda Mecánica es una perturbación que viaja por un material o sustancia que es un medio de la onda.
Por ejemplo, cuando se pulsa una cuerda tensa, la perturbación provocada se propaga a lo largo de la misma en forma de un pulso ondulatorio. Esta perturbación consiste en la variación de la forma de la cuerda a partir de su estado de equilibrio.
Al viajar la onda por el medio, las partículas que forman el medio sufren desplazamientos de varios tipos, dependiendo de la naturaleza de la onda.
Por ejemplo, cuando se pulsa una cuerda tensa, la perturbación provocada se propaga a lo largo de la misma en forma de un pulso ondulatorio. Esta perturbación consiste en la variación de la forma de la cuerda a partir de su estado de equilibrio.
Al viajar la onda por el medio, las partículas que forman el medio sufren desplazamientos de varios tipos, dependiendo de la naturaleza de la onda.
Cuando la perturbación es perpendicular a la dirección de propagación se denomina onda transversal, y cuando la perturbación es paralela a la dirección de propagación se denomina onda longitudinal.
Todas las ondas mecánicas requieren:
- Alguna fuente que cree la perturbación.
- Un medio en el que se propague la perturbación.
- Algún medio físico a través del cual elementos del medio puedan influir uno al otro.
- Ondas longitudinales
Esta forma de movimiento ondulatorio es característica de la propagación de las ondas de sonido en el aire, en los líquidos no viscosos y en los gases en general, por lo que también reciben el nombre de ondas sonoras.
Las ondas longitudinales son aquellas en que la propagación y la vibración de las partículas tienen el mismo sentido.
- Ondas transversales
Las ondas transversales tienen lugar, sobre todo, en sólidos y líquidos viscosos, aunque en estos materiales también es posible la propagación de ondas longitudinales.
5.2 Ondas periódicas
Las ondas más interesantes de la naturaleza son periódicas. Eso quiere decir que no es una única perturbación la que viaja, sino que son muchas (muchísimas) perturbaciones, una atrás de la otra, todas iguales y equiespaciadas. Eso es una onda periódica.
En este clase de ondas,las partículas se mueven perpendicularmente a la dirección de propagación de la onda. La forma más simple de onda periódica es la onda armónica (sinusoidal).
5.3 Descripción matemática de una onda
Desde un punto de vista matemático, la onda más sencilla o fundamental es la onda sinusoidaldescrita por la función

donde es la amplitud de una onda (la elongación máxima o altura de la cresta de la onda). Las unidades de amplitud dependen del tipo de onda — las ondas en una cuerda tienen una amplitud expresada como una distancia (metros), las ondas sonoras como presión (pascales) y ondas electromagnéticas como la amplitud del campo eléctrico (voltios/metros). La amplitud puede ser constante, o puede variar con el tiempo y/o posición.
es la amplitud de una onda (la elongación máxima o altura de la cresta de la onda). Las unidades de amplitud dependen del tipo de onda — las ondas en una cuerda tienen una amplitud expresada como una distancia (metros), las ondas sonoras como presión (pascales) y ondas electromagnéticas como la amplitud del campo eléctrico (voltios/metros). La amplitud puede ser constante, o puede variar con el tiempo y/o posición.

La longitud de una onda
simbolizada por ) es la distancia entre dos crestas o valles seguidos. Se mide en unidades de longitud, tales como el metro(m), sus múltiplo o submúltipos según convenga. Así, en la óptica, la longitud de onda de la luz se mide en nanómetros.
) es la distancia entre dos crestas o valles seguidos. Se mide en unidades de longitud, tales como el metro(m), sus múltiplo o submúltipos según convenga. Así, en la óptica, la longitud de onda de la luz se mide en nanómetros.

Un numero de una onda
angular puede ser asociado con la longitud de onda por la relación:
puede ser asociado con la longitud de onda por la relación:

El periodo
 es el tiempo requerido para que el movimiento de oscilación de la onda describa un ciclo completo. La frecuencia
es el tiempo requerido para que el movimiento de oscilación de la onda describa un ciclo completo. La frecuencia  es el número de ciclos completos transcurridos en la unidad de tiempo (por ejemplo, un segundo). Es medida en hercios. Matemáticamente se define sin ambigüedad como:
es el número de ciclos completos transcurridos en la unidad de tiempo (por ejemplo, un segundo). Es medida en hercios. Matemáticamente se define sin ambigüedad como:

En otras palabras, la frecuencia y el periodo de una onda son recíprocas entre sí.

donde
La longitud de una onda
simbolizada por
Un numero de una onda
angular
El periodo
En otras palabras, la frecuencia y el periodo de una onda son recíprocas entre sí.
5.4 Rapidez de una onda transversal
La velocidad de propagación de las ondas
mecánicas depende de la elasticidad del medio en el cual se propagan. Los
materiales menos densos ofrecen menor resistencia al movimiento de las ondas.
La elasticidad de
una cuerda oscilante está determinada por sus propiedades mecánicas y por su
tensión F. Su densidad lineal 4, está definida por:
donde m es la masa
de la cuerda y L es la longitud total de la cuerda.
La velocidad de
propagación de una onda transversal está dada por la siguiente expresión:
En esta ecuación se
puede observar que si se mantiene constante la tensión F de la cuerda, la
velocidad de las ondas dependerá inversamente proporcional a la raíz cuadrada
de la densidad lineal de masa de la cuerda.
Por otra parte, si
se conocen la frecuencia y la longitud de una onda/ la velocidad de una onda se
puede calcular de acuerdo con la siguiente expresión:
 (3)
(3)
En un medio con
propiedades mecánicas invariables, la velocidad de propagación de una onda es
constante/ de acuerdo con la expresión (2).
Por esta razón se puede observar en la ecuación (3) que sí la longitud
de una onda se incrementa, la frecuencia disminuye y viceversa.
5.5 Energía del movimiento ondulatorio
Un medio en el que se propaga un movimiento ondulatorio posee energía, que es en parte cinética y en parte potencial.
La energía cinética del elemento de masa  (m es la densidad lineal de masa) situado en Q será:
(m es la densidad lineal de masa) situado en Q será:
Ahora bien como todos los elementos de masa tienen la misma energía
La potencia total transferida será 

teniendo en cuenta que  podemos escribir la potencia de una onda unidimensional como:
podemos escribir la potencia de una onda unidimensional como:
En el desarrollo anterior, se ha evitado, hacer referencia a la sección S de la cuerda, pues hemos preferido expresarnos en términos de densiades lineales de masa.
Si hacemos intervenir la densidad volúmica de masa ( ), para ello , basta que tengamos en cuenta que
), para ello , basta que tengamos en cuenta que  , de este modo la expresión que resulta es más general, puesto que será aplicable a todo tipo de ondas que se propaguen en dos o tres dimensiones.
, de este modo la expresión que resulta es más general, puesto que será aplicable a todo tipo de ondas que se propaguen en dos o tres dimensiones.
5.6 Interferencia de ondas, condiciones de frontera y superposición
- La interferencia constructiva
Ocurre cuando en un punto de un medio interfieren ondas que tienen un desplazamiento en la misma dirección. Las ondas se refuerzan mutuamente cuando se superpone una cresta a otra cresta (o un valle a otro valle). Como en la figura de arriba, ambas ondas (la roja y la azul) tienen la forma de una cresta, el medio tiene un desplazamiento hacia arriba que es mayor que el desplazamiento de las dos ondas que interfieren. El desplazamiento del medio es mostrado en color verde.

- La interferencia destructiva
- Principio de Superposición
Combinar los desplazamientos de los pulsos individuales en cada punto para obtener el desplazamiento real es un ejemplo del principio de superposición: cuando dos ondas se traslapan, el desplazamiento real de cualquier punto de la cuerda en cualquier instante se obtiene sumando el desplazamiento que tendría el punto si sólo estuviera presente la primera onda, con el desplazamiento que tendría si sólo estuviera presente la segunda. Dicho de otro modo, la función de onda y(x, t) que describe el movimiento resultante en esta situación se obtiene sumando las dos funciones de onda de las ondas individuales.
5.7 Ondas estacionarias en una cuerda
Las ondas estacionarias en una cuerda son el resultado de la
superposición de ondas armónicas propagándose por una cuerda
en la que ambos extremos están fijos. Si se hace vibrar uno de los
extremos siguiendo un Movimiento Armónico Simple (MAS)
perpendicular a la cuerda, éste se propaga en forma de onda
armónica por la cuerda. Al llegar a los extremos fijos, la onda se
refleja de forma que al final en la cuerda tendrá lugar la
superposición de las ondas que da lugar a la onda estacionaria.
Suponiendo inicialmente una cuerda fija en su extremo izquierdo,
que hacemos coincidir con el origen de coordenadas, podemos
representar las ondas incidente (que viaja hacia la izquierda) y
reflejada (que viaja hacia la derecha) respectivamente como :
donde y0 es la amplitud del MAS, f es la frecuencia del MAS y λ es el Longitud de Onda. f y λ se
relacionan a través de la velocidad de propagación de la onda v = λ f = TL / m , donde T es la tensión
a la que está sometida la cuerda, y m y L son su masa y longitud. De la superposición de ambas ondas
resulta una onda estacionaria, descrita por la ecuación:
la cual explica la aparición de nodos (N), donde la cuerda está siempre en reposo, y antinodos, o valles,
(A), donde las oscilaciones de la cuerda alcanzan su máxima amplitud (2y0). La posición de dichos
nodos xN se puede obtener a partir de la ecuación anterior (ver más abajo). Así mismo, al imponer en
dicha ecuación que el extremo derecho de la cuerda también sea fijo, se obtiene el conjunto de
frecuencias discretas fn (o armónicos) para las cuales la cuerda soporta ondas estacionarias:
5.8 Modos normales de una cuerda
 Un modo normal de un sistema oscilatorio es la frecuencia a la cual la estructura deformable oscilará al ser perturbada. Los modos normales son también llamados frecuencias naturales o frecuencias resonantes. Para cada estructura existe un conjunto de estas frecuencias que es único.
Un modo normal de un sistema oscilatorio es la frecuencia a la cual la estructura deformable oscilará al ser perturbada. Los modos normales son también llamados frecuencias naturales o frecuencias resonantes. Para cada estructura existe un conjunto de estas frecuencias que es único.El concepto de modos normales también es aplicable en teoría ondulatoria, óptica y mecánica cuántica.
Cuando se pulsa una cuerda de guitarra, se produce una onda en ella; esta onda se refleja una y otra vez en los extremos de la cuerda, formando una onda estacionaria.
Ésta, a la vez, produce una onda sonora en el aire, cuya frecuencia está determinada por las propiedades de la cuerda.
Un modo normal de un sistema oscilante es un movimiento en el que todas las partículas del sistema se mueven senoidalmente con la misma frecuencia. En el caso de un sistema compuesto por una cuerda de longitud L fija en ambos extremos, cada una de las longitudes de onda corresponde al patrón y a la frecuencia de un posible modo normal.
Hay un número infinito de modos normales, cada uno con su frecuencia y patrón de vibración característicos. La figura 15.26 muestra los primeros cuatro patrones de modo normal y sus respectivas frecuencias y longitudes de onda. En contraste, un oscilador armónico, que sólo tiene una partícula oscilante, tiene un solo modo normal y una sola frecuencia característica.
En este apartado, obtendremos la fórmula que nos da las frecuencias de los modos de vibración de una cuerda de longitud L, sujeta por sus extremos.
5.9 Fuerzas de fricción. Dinámica del movimiento circular.
- Fuerza de fricción.
Empíricamente se ha establecido que la fuerza de fricción cinética es proporcional a la fuerza normal N, siendo k la constante de proporcionalidad, esto es, f = N.
- Dinámica del movimiento circular

En un movimiento de este tipo, su trayectoria es circular y, según se vio, existe una relación sencilla entre la componente normal de la aceleración, la velocidad lineal de la partícula y el radio de la trayectoria. En todo movimiento la aceleración puede descomponerse en dos componentes:
1) Aceleración normal (an) responsable del cambio de dirección (si an = 0 la trayectoria es una recta)
2) Aceleración tangencial (at) responsable del cambio en la velocidad lineal con la que se mueve el objeto.
5.10 Fuerzas fundamentales es de la naturaleza.
 Fuerza de gravedad
Fuerza de gravedadEsta es una fuerza puramente atractiva, ya que dos cuerpos con masa siempre tienden a atraerse por la fuerza de gravedad, a diferencia de otras fuerzas en las que también se pueden rechazar los objetos. Esta fuerza es la que mantiene a los planetas orbitando y girando alrededor del Sol, así como también por ejemplo a nuestro satélite natural, la Luna, que orbita alrededor de la Tierra. El gran Albert Einstein clarificó el concepto que teníamos de la fuerza de gravedad en su teoría general de la relatividad, como la curvatura del espacio-tiempo causada alrededor de cualquier objeto que tuviera masa.
Fuerza de Electromagnética
 Una de las fuerzas que mejor conocemos y también a las que más habituados estamos, esta se da a través de partículas que se encuentran cargadas eléctrica mente. Aquí, sin embargo, podemos tener una fuerza de atracción (partículas de diferente carga) o una fuerza de repulsión (misma carga). En el pasado se consideraba a la fuerza eléctrica y magnética como fuerzas distintas, pero James Clark Maxwell las unificó en 1864, en su llamada ecuación de Maxwell.
Una de las fuerzas que mejor conocemos y también a las que más habituados estamos, esta se da a través de partículas que se encuentran cargadas eléctrica mente. Aquí, sin embargo, podemos tener una fuerza de atracción (partículas de diferente carga) o una fuerza de repulsión (misma carga). En el pasado se consideraba a la fuerza eléctrica y magnética como fuerzas distintas, pero James Clark Maxwell las unificó en 1864, en su llamada ecuación de Maxwell.Fuerza nuclear débil
 Tal como su nombre lo indica, la fuerza nuclear débil o "interacción débil" es una fuerza débil si lo comparamos con las otras tres anteriores, aunque tiene una función muy importante. Esta fuerza actúa a nivel de los núcleos atómicos y es la que permite la fusión de, por ejemplo, el hidrógeno, que es lo que nos permite no solo disfrutar de la luz del Sol, sino concebir la existencia misma tal como lo hacemos, siendo verdaderamente fundamental.
Tal como su nombre lo indica, la fuerza nuclear débil o "interacción débil" es una fuerza débil si lo comparamos con las otras tres anteriores, aunque tiene una función muy importante. Esta fuerza actúa a nivel de los núcleos atómicos y es la que permite la fusión de, por ejemplo, el hidrógeno, que es lo que nos permite no solo disfrutar de la luz del Sol, sino concebir la existencia misma tal como lo hacemos, siendo verdaderamente fundamental.Fuerza nuclear fuerte

Esta es la más fuerte de todas las fuerzas, esta fuerza permite a los nucleones (los protones y los neutrones) mantenerse unidos a pesar de la fuerza de repulsión que existe entre ellas (los protones tienen la misma carga eléctrica positiva por lo que se rechazan mutuamente). Esta fuerza se considera de corto alcance, ya que permite que los protones del núcleo se encuentren unidos, por lo que solo afecta al mismo núcleo.
5.11 Aplicaciones.







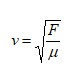




Comentarios
Publicar un comentario